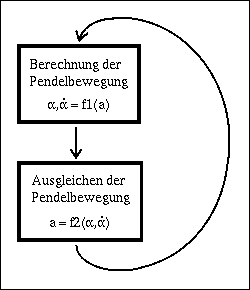
Diese aufrichtende Kraft beeinflusst dann im nächsten Iterationsschritt wiederum Winkel und -geschwindigkeit:
________________
Die Funktion f1 entspricht dabei der Simulation der Pendelbewegungen, f2 ist für das Ausbalancieren derselben zuständig. Diese Schleife kann auch im C-Quellcode der Curses-Version des Programmes gefunden werden:
while (alpha>=0.0 && alpha<=pi){
...
/* f1: Pendel-Verhalten nach Ch. Ziegaus */
Fres = sqrt(sqr(Fg) + sqr(Fa));
rho = alpha - arccos(Fa/Fres);
Fz = sin(rho) * Fres;
deltaAlpha = Fz/(2.0*m*l)*sqr(deltaT) + alphaDot*deltaT;
alphaDot = Fz/(m*l)*deltaT + alphaDot;
alpha = alpha + deltaAlpha;
/* f2: Ausgleichen der Pendelbewegung */
Fa = m*balance(alpha,alphaDot)*a0;
...
}
Hier werden zuerst Winkel (alpha) und
Winkelgeschwindigkeit (alphaDot) berechnet, anschliessend
wird mit Hilfe der Funktion balance() die Balancier-Kraft
Fa errechnet, mit der der Wagen am Fußpunkt des Pendels
beschleunigt wird.
balance() ist also für das eigentliche
Balancieren verantwortlich, sie bewerkstelligt dies anhand einer
Fuzzy-Steuerung. Diese besteht aus den folgenden Teilen:
alphaalpha befindet. Dazu wird für jeden der möglichen
Bereiche (NB, NS, NM, ZE, PS, PM, PB) abgeprüft, zu welchem Grad der
Winkel in diesem Bereich liegt. Dieser Grad kann zwischen 0.0 und 1.0
liegen, er wird im Array b_alpha[] für jeden Bereich
festgehalten.
Die folgende Grafik soll dies verdeutlichen:
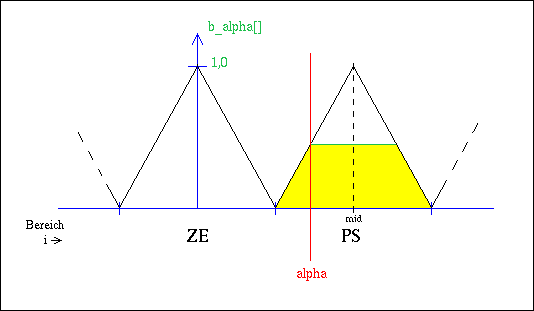
Da sich die Bereich überschneiden können, kann alpha
in mehreren Bereichen einen Grad >0 haben.
Der oben beschriebene Berechnungsvorgang wird im
C-Quellcode der Curses-Version
durch das folgende Code-Fragment abgedeckt:
/* Gewichte von alpha ausrechnen */
for(i=0;i<NRANGES;i++){
if((b_alpha_u[i] > alpha) && (alpha > b_alpha_l[i])){
mid = (b_alpha_u[i]+b_alpha_l[i])/2.0;
if(alpha>mid){
/* linke Haelfte */
b_alpha[i] = 1.0-(alpha-mid)/(b_alpha_u[i]-mid);
}else{
/* rechte Haelfte */
b_alpha[i] = (alpha-b_alpha_l[i])/(mid-b_alpha_l[i]);
}
}else{
b_alpha[i] = 0.0;
}
}
i wird dabei über alle Bereiche von 0=NB bis
7=PS(=NRANGES) iteriert. Liegt der Winkel alpha
im jeweiligen Bereich (dessen untere und obere Grenze in
b_alpha_l[] bzw. b_alpha_u[] stehen), so wird
in b_alpha[i] festgehalten, wie stark sich der Winkel in
der Mitte des jeweiligen Bereichs b_alpha[i] auf
0.0 gesetzt.
Während der Simulation werden die so berechneten Werte sowohl in tabellarischer als auch in grafischer Form angezeigt.
Grad der Auslenkung der Winkelgeschwindigkeit
Hier wird analog zur Berechnung der Winkel-Grade vorgegangen, die
Grenzen der einzelnen Bereiche stehen in den Arrays
alphaDotb_alphaDot_l[] und b_alphaDot_u[]. Die
berechneten Grade der einzelnen Bereiche werden im Array
b_alphaDot[] gespeichert und während der Simulation
ebenfalls in
tabellarischer und
grafischer Form angezeigt.
Wenn
Aufgrund der "und"-Verknüpfung der beiden Bedingungen wird
Im C-Quellcode der Curses-Version
sieht dies so aus:
Dann werden nacheinander sämtliche Regeln angewandt.
Wie oben erwähnt wird der Betrag der Kraft aus dem Minimum der Grade
von Winkel und Winkelgeschwindigkeit ermittelt (aufgrund der
"und"-Verknüpfung). Falls bereits eine Regel auf den angesprochenen
Bereich gewirkt hat, so wird die maximale Kraft der beiden zur Berechnung
der Ausgleichskraft verwendet.
Im vorliegenden Fall wurden dabei die einzelnen Bereiche mit Gewichten
versehen, mit denen die einzelnen Grade Multipliziert und anschliessend
aufaddiert wurden:
Anwenden der Fuzzy-Regeln
Nachdem nun die Grade von alpha und alphaDot
bestimmt sind ist es möglich, die Regeln zur Aussteuerung des Pendels
anzuwenden. Diese treffen für Kombinationen von Winkel und
Winkelgeschwindigkeit Aussagen darüber, wie die Ausgleichkraft
Fa beschaffen sein muß, um das Pendel aufzurichten, z. B.:
alpha=PS und alphaDot=NS, dann setze
Fa=ZE.
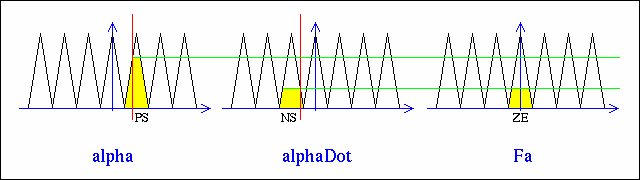
Fagleich dem kleineren der beiden Werte alpha
und alphaDot gesetzt. Dies soll auch nochmal in der
folgenden Grafik veranschaulicht werden:
/* Regeln anwenden */
for(i=0;i<NRANGES;i++){
b_Fa[i] = 0.0;
}
for(i=0;i<NRULES;i++){
b_Fa[b_rule_a[i]] = Max(b_Fa[b_rule_a[i]],
Min(b_alpha[b_rule_alpha[i]],
b_alphaDot[b_rule_alphaDot[i]]));
}
Dabei wird Fa zuerst für alle Bereiche von 0 (=NB) bis
NRULES (=7=PB) auf 0 gesetzt, d. h. es soll keine Kraft wirken.
b_rule_a[] enthält dabei die Aussage, wie stark und in
welche Richtung die Kraft wirken soll, b_rule_alpha[]
und b_rule_alphaDot[] bestimmen, unter welchen Bedingungen
diese Kraft angewandt werden soll.
Defuzzifizierung
Nachdem durch das Anwenden der Regeln ein oder meist sogar mehrere
Aussagen über die Stärke der Ausgleichskraft Fa getroffen
wurden, soll nun in einem letzten Schritt ein Zahlenwert
(max) aus den gesamten Aussagen errechnet werden.
/* Mittelwert ausrechnen */
max=0.0;
for(i=0;i<NRANGES;i++){
max =max + (i-(NRANGES/2))*b_Fa[i];
}
Hier geht's zur Einführung zum Fuzzy-Pendel
zurück, und hier gibt's Informationen
über die Implementierung.
Hubert Feyrer, hubert.feyrer@informatik.fh-regensburg.de